1673, Amsterdam. Un bulbe de tulipe se négocie à prix d’or, et la spéculation bat son plein dans les salons feutrés de la bourgeoisie néerlandaise. Derrière cette frénésie, un outil financier discret, mais redoutable : l’option. La mécanique qui sous-tend ce marché fascinant n’a pas fini de faire parler d’elle, tant elle façonne encore aujourd’hui les stratégies et les fortunes.
Un détour par la folie des tulipes
Au XVIIe siècle, les Pays-Bas voient s’embraser la passion pour la tulipe, symbole d’ascension sociale. Les producteurs, soucieux de sécuriser leurs gains, acquièrent des options de vente pour se prémunir contre la chute des prix. Les grossistes, eux, cherchent à se protéger de la flambée en achetant des options d’achat. Rapidement, un marché secondaire d’options s’organise, offrant aux investisseurs la possibilité de parier sur l’évolution du prix de ces bulbes prisés. Mais cette dynamique effrénée finit par se retourner : la bulle spéculative éclate, laissant le pays exsangue et marquant l’histoire économique d’une empreinte indélébile.
Tour de vis sur les marchés : l’option bannie
La déflagration de la crise des tulipes a des répercussions durables. Malgré la structuration d’un marché d’options à Londres dès 1600, le vent tourne : États-Unis, Angleterre, Japon interdisent tour à tour la négociation de ces instruments. En Angleterre, la prohibition s’étendra du début du XVIIIe siècle jusqu’à la fin du XIXe. Les options, jugées trop risquées ou trop spéculatives, disparaissent temporairement des écrans radars officiels.
Russel Sage, pionnier des options modernes
À la fin du XIXe siècle, Russel Sage, financier américain, fonde une société de courtage dédiée aux options de gré à gré. Il sera le premier à établir un lien structuré entre le prix d’une option, la valeur de son actif sous-jacent et le niveau des taux d’intérêt. Sage s’appuie sur la parité call-put pour monter des prêts synthétiques, ajustant habilement les paramètres de ses contrats pour fixer les taux d’intérêt de ses offres. Cette vision novatrice contribue à faire évoluer le marché. À mesure que le siècle s’achève, courtiers et opérateurs multiplient les initiatives pour attirer vendeurs et acheteurs d’options, fédérant leurs réseaux afin de générer la liquidité qui manque encore cruellement.
Le marché organisé : naissance d’un système
Le marché des options poursuit sa mutation, longtemps dominé par des courtiers concluant des contrats de gré à gré. Leur marge se fait sur l’écart entre le prix d’achat (bid) et le prix de vente (ask). Concrètement, ils achètent à bas prix, revendent plus cher, et vivent de ce différentiel, appelé spread bid-ask.
Quand Chicago change la donne
1968, le Chicago Board of Trade constate que l’activité sur les marchés à terme s’essouffle. Pour relancer la machine, il lance le projet d’un marché réglementé d’options cotées. C’est ainsi qu’en 1973, le Chicago Board of Options Exchange (CBOE) voit le jour. À ses débuts, seuls quelques contrats d’options d’achat (calls) sont proposés, et le marché peine à décoller : l’absence de méthode fiable pour évaluer une option et l’ampleur des écarts de prix freinent les échanges. Cette même année, Fisher Black et Myron Scholes publient une formule qui va révolutionner la finance : le calcul rigoureux du prix d’une option devient enfin possible. Dès 1974, la moyenne quotidienne des options échangées franchit la barre des 20 000. Quatre siècles après la folie des tulipes, les options trouvent leur place sur un marché régulé.
Mais concrètement, qu’est-ce qu’une option ? Il s’agit d’un contrat négocié en bourse (option cotée) ou directement entre deux parties (OTC), qui donne à l’acheteur le droit, sans obligation, d’acheter (call) ou de vendre (put) un actif sous-jacent à un prix fixé d’avance (strike), soit pendant une période donnée (option américaine), soit à une date précise (option européenne). Chaque paramètre du contrat, prix d’exercice, échéance, est déterminé dès la signature. Les options américaines sont exerçables à tout moment avant l’échéance, alors que les européennes ne le sont qu’à maturité. Exercer une option revient à utiliser son droit d’acheter ou de vendre l’actif sous-jacent au prix convenu.
Un agriculteur face au risque
Pour saisir l’utilité d’une option, prenons un exemple concret. Un agriculteur, dont la récolte sera vendue plus tard dans l’année, redoute une chute de prix sur le marché. Il achète alors une option de vente qui couvre la période autour de la moisson, garantissant ainsi un prix plancher pour sa production, quelle que soit l’évolution du marché.
Le bijoutier qui verrouille ses coûts
Autre exemple : un bijoutier, obligé d’acheter régulièrement de l’or, anticipe une hausse des cours. Il acquiert une option d’achat qui lui permettra, le moment venu, d’acheter son métal précieux à un prix maximum fixé à l’avance, le mettant à l’abri des envolées tarifaires.
Pour comprendre comment se forme le prix d’une option (la prime), il faut examiner plusieurs paramètres :
- La valeur de l’actif sous-jacent
- La volatilité de ses rendements
- Le niveau des taux d’intérêt
- Le temps qui s’écoule jusqu’à l’échéance
Les fameux « Grecs », Delta, Gamma, Vega, Rho, permettent aux professionnels de mesurer la sensibilité de la prime à chacun de ces facteurs.
Delta : la sensibilité au mouvement du sous-jacent
Le Delta indique comment le prix de l’option réagit aux variations du sous-jacent. Pour un call, si la valeur du sous-jacent augmente, la prime grimpe également. À l’inverse, pour un put, la prime baisse si le sous-jacent prend de la valeur. Imaginons un call avec un Delta de 10 €. Si l’actif sous-jacent augmente de 2 €, la prime de l’option bondit de 20 €.
Gamma : la courbure de la réaction
Gamma mesure la variation du Delta lui-même, c’est-à-dire la sensibilité de l’option aux changements non linéaires du sous-jacent. Plus le sous-jacent s’éloigne de sa valeur d’origine, plus l’effet du Gamma se fait sentir. Par exemple, un call doté d’un Gamma de 2 € : si le sous-jacent baisse de 2 €, la prime varie de 4 € (0,5 × 2 × (−2)2). Ce qui compte ici, c’est l’ampleur du mouvement, pas sa direction.
Vega : l’impact de la volatilité
Vega s’intéresse à la volatilité implicite du sous-jacent. Si la volatilité grimpe, la prime de l’option augmente, toutes choses égales par ailleurs. Exemple : un call avec un Vega de 5 €. Si la volatilité implicite progresse de 2 %, la prime augmente de 10 €.
Thêta : l’érosion du temps
Thêta mesure l’effet du temps qui passe. Pour un call, à mesure que l’échéance approche, la prime perd de la valeur. Prenons un call avec un Thêta de −0,10 €. Chaque jour écoulé, la prime de l’option se réduit de 0,10 €.
Rho : l’influence des taux d’intérêt
Rho quantifie la sensibilité de l’option aux variations des taux d’intérêt. Pour un call, une hausse des taux fait augmenter la prime. Exemple : un call avec un Rho de 3 €. Si la courbe des taux progresse de 2 %, la prime s’apprécie de 6 €.
Gérer un portefeuille d’options : l’art de l’équilibre
Sur les marchés d’options organisés, comme EUREX ou Liffe, le teneur de marché doit afficher en continu ses prix d’achat et de vente. Son profit provient du différentiel entre ces deux prix. Chaque opération vient s’ajouter à son portefeuille, obligeant le market maker à ajuster dynamiquement ses positions. Les salles de marché des grandes banques ne cherchent pas à prendre des paris directionnels risqués. Elles neutralisent donc leur exposition, notamment le Delta, en achetant ou en vendant les actifs sous-jacents ou des contrats à terme.
Si l’ajustement du Delta peut se faire de façon relativement simple, la gestion des autres sensibilités (Gamma, Vega, Thêta) exige une surveillance et des ajustements constants. Pour cela, il faut acheter ou vendre des options au fil de la journée, afin de maintenir un portefeuille aussi proche que possible de la neutralité par rapport à l’ensemble des risques.
Les Grecs et l’approximation de Taylor
Pour exprimer la valeur d’un call en fonction de ses paramètres, on a recours à l’approximation de Taylor, ce qui permet d’évaluer l’impact de variations infinitésimales sur le prix de l’option. Cette approche s’appuie sur la formule :
C = V(t, S, sigma, r)
On peut alors écrire, en notant les variations :
dC = (∂C/∂t)dt + (∂C/∂S)dS + (1/2)(∂²C/∂S²)dS² + (∂C/∂sigma)dσ + (∂C/∂r)dr
Soit, en résumé :
dC = Thêta·dt + Delta·dS + (1/2)Gamma·dS² + Vega·dσ + Rho·dr
Les Grecs offrent donc une vision fine de la façon dont le prix d’un call évolue lorsque ses variables de référence changent, même très légèrement.
Visualiser les résultats
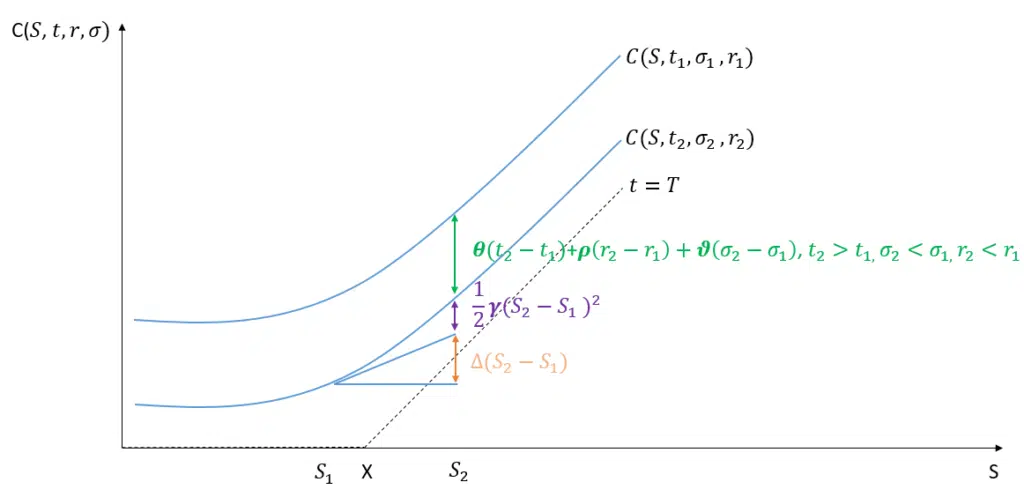
La démonstration de Black et Scholes (1973) formalise mathématiquement le prix d’une option. On considère un portefeuille autofinancé composé d’une option V(S, t) et d’une quantité Delta du sous-jacent S :
P(t) = V(S, t) + Delta·S(t)
Plusieurs hypothèses sont posées :
- Le sous-jacent suit un processus d’Ito : dS/S = μ dt + σ dZ, avec dZ ~ N(0, dt)
- Le sous-jacent ne verse pas de dividendes
- Le taux sans risque reste constant
- Il n’y a pas de frais de transaction
- Le rendement suit une loi normale logarithmique
- L’option est de type européenne
- Le marché est efficient
Le lemme d’Ito permet d’obtenir la dynamique de la valeur de l’option :
dV = (∂V/∂t + μS∂V/∂S + (1/2)σ²S²∂²V/∂S²)dt + σS∂V/∂S dZ
Le portefeuille étant autofinancé, seules les variations des actifs le composant comptent :
dP = dV + Delta·dS
En développant, on impose que la composante aléatoire s’annule pour obtenir un portefeuille sans risque : cela donne Delta = −∂V/∂S.
Le portefeuille sans risque doit alors rapporter le taux sans risque :
dP = rPdt
On en déduit l’équation de Black-Scholes :
∂V/∂t + (1/2)σ²S²∂²V/∂S² + rS∂V/∂S − rV = 0
Avec les conditions limites suivantes :
- V(0, t) = 0
- V(S, t) ~ S lorsque S tend vers l’infini
- À maturité, V(S, T) = max(S, K, 0)
En opérant un changement de variables :
x = ln(S/K)
τ = (σ²/2)(T, t)
V(S, t) = K·v(x, τ)
k = r/(σ²/2)
v(x, τ) = exp(αx + βτ)·u(x, τ)
α = −(k, 1)/2
β = −((k + 1)²)/4
L’équation se ramène à :
∂u(x, τ)/∂τ = ∂²u(x, τ)/∂x²
On reconnaît l’équation de la chaleur, dont la solution intégrale s’écrit :
u(x, τ) = (1/√(2π τ)) ∫−∞+∞ u₀(s)·exp(−(x − s)²/(4τ)) ds
Avec :
d₁ = [ln(S/K) + (r + σ²/2)(T − t)] / (σ√(T − t))
d₂ = d₁ − σ√(T − t)
La fonction φ(x) = (1/√(2π)) ∫−∞x exp(−y²/2) dy correspond à la probabilité pour une variable normale centrée réduite.
La formule finale du prix d’un call européen en t sur un sous-jacent S s’écrit alors :
C(S, t) = S·φ(d₁) − K·exp(−r(T − t))·φ(d₂)
Le calcul de la valeur d’une option, autrefois affaire d’intuition et de paris, devient alors un exercice de rigueur, capable de résister à toutes les tempêtes du marché. L’option reste un terrain de jeu technique, où chaque variable compte et chaque choix pèse, un univers où la précision fait la différence entre coup de maître et faux pas.
